The Drunken Salesman: Applying the Travelling Salesperson Problem to Manchester Breweries

· 13 min read

Introduction

Note: In England in 2018/19 there were 1.26 million hospital admissions related to alcohol consumption, making up 7.4% of all hospital admissions. For more facts and support about alcohol check out the dedicated NHS website and please drink responsibly!

I’m a fan of craft beer. And coding. To combine these two I decided to apply the travelling salesperson problem to the brewery taprooms in Manchester, where I used to live, using a combination of Google Maps, Openrouteservice, Python, and Julia. If you want to skip all of the details on how I did this, then the final route can be found at the bottom of this post. The code from this post can be found here.

Before getting into the details of what I did, let’s first define the travelling salesperson problem

Given a finite number of cities along with the cost of travel between each pair of them, and with the object of finding the cheapest way of visiting all the cities and returning the original point of departure

and has been studied since the 1930’s - understandable considering how useful the solution is!

A mathematical formulation is: Given a set of $n$ cities to be visited with distance between cities $i$ and $j$ given by $c_{ij}$. Introduce $y_{ij}$ for each $(i,j)$ s.t. \begin{equation} y_{i,j} = \begin{cases} 1 \quad \text{if city $j$ is visited immediately after $i$,}\newline 0 \quad \text{otherwise.}\newline \end{cases} \end{equation} The objective function is then given by $\min \sum c_{ij}y_{ij}$, and we have the following constraints to ensure the solution is valid: \begin{align} \sum_{j} y_{ij} &= 1, \quad i = 0,1,\dots,n-1\newline \sum_{i} y_{ij} &= 1, \quad j = 0,1,\dots,n-1\newline \sum_{i}\sum_{j} y_{ij} &\leq |S|-1 \quad S \subset V, 2\leq|S|\leq n-2, \end{align} where $G = (V,E)$ is the graph with vertices $V$ and edges $E$ and $S$ is the set of all tours of $G$. The travelling salesperson problem can be either symmetric $c_{ij} = c_{ji} \forall i,j$ or asymmetric where the equality does not hold.

To compute all possible solutions and find the best is $\mathcal{O}(n!)$, which is intolerably slow, and therefore heuristic algorithms are typically used to find a ‘good’ solution. A simple example of such an algorithm is the nearest neighbour algorithm, which simply chooses the nearest point to the previous chosen point to construct a path. This gives $n$ different solutions as the initial point can be any of the ‘cities’ in our problem. For certain arranged points this algorithm can actually return the worst possible solution, and therefore this may not be a great algorithm to use.

The nearest neighbour is an example of a route construction algorithm: a solution is gradually built by adding a new city at each step. Other examples are the greedy algorithm, where a route is constructed by repeatedly selecting the shortest edge that does not create a loop within the route, and the cheapest insertion algorithm which starts with a subset of points and inserts a new point into the route between two consecutive points such that the length of the new route is minimised.

Other heuristic algorithms can be classified as tour improvement algorithms: a feasible solution is gradually improved at each iteration by exchanging cities. The 2-opt algorithm randomly removes 2 edges from a route and then reconnects them in such a way that the route is still feasible (and the value of the objective function is reduced), continuing until no further improvements are possible. This can be generalised to the k-opt algorithm. For more details on the travelling salesperson problem you can check out this link from Northwestern University.

Outline

Applying the travelling salesperson problem to the Manchester taprooms is a relatively straightforward procedure that can be split into the following steps:

  1. Find the geographic coordinates of the taprooms (Google Maps) and put them in a csv file.
  2. Find the walking time between each pair of locations (Python - Openrouteservice).
  3. Solve the TSP (Julia).
  4. Map the points and route (Python - Folium).

You may be asking why I switched to Julia to solve the TSP before going back to Python? Unfortunately I could not get the algorithms I was using in Python to give me a good solution, despite a lot of attempts at tweaking the parameters of the optimisation algorithms I was using. Julia was also much faster at computing a solution and I’d never used Julia before so it gave me an incentive to try out a new language. Unfortunately the Openrouteservice API has not been implemented in Julia, so I performed this in Python.

Finding the coordinates

The first step was to generate a list of taprooms in Manchester. I decided that the tour should begin and end at Piccadilly station, so I came up with 22 locations in total: Alphabet Brewing Company, Beatnikz Republic Brewery, Beatnikz Republic Bar, Beer Nouveau, BrewDog, BrewDog Outpost, Cloudwater, Gas Lamp (Pomona Island), Gasworks, Knott (Wander Beyond), Manchester Union, Marble Arch (Marble Beers), Northern Monk Refectory, Ol, Piccadilly Station, Runaway, Seven Bro7hers, Smithfield Market Tavern/Jack in the Box (Blackjack), Thomas St Beerhouse (Marble Beers), Track/Squawk. Most of these locations were picked based on my local knowledge however I also used this handy map.

A few notes on these: Smithfield Market Tavern & Jack in the Box are located next door to each other and are therefore given as a single location, they’re also operated by the same brewery. Track and Squawk are on the 3rd and 4th floor, respectively, of the same building and are therefore listed as a single location. At the time of writing, Track & Squawk were both closed due to a problem with the building, but they have not been removed in anticipation of them reopening.

Finding out the coordinates of these places was the most manual part of the process. I went in and searched for each place individually in Google Maps. To get the coordinates you can either drop a pin at the location (or very close to) using a long click on your mouse, or you can right click and click on ‘What’s here?'. It is possible to automate this using the Google Maps Geocoding API however there is a cost to this. Due to the small number of points I decided to use the manual method. Another option is to use the Open Postcode Geo API, which returns coordinates based on postcodes. This is very simple and requires reading from a url. For example the following code shows how to use the API with the postcode for Piccadilly Station.

using HTTP
using JSON
postcode_json = JSON.parse(String(HTTP.get("http://api.getthedata.com/postcode/NG92LG").body))
picc_lat = postcode_json["data"]["latitude"]
picc_lon = postcode_json["data"]["longitude"]

The downside of this is that I didn’t know the postcodes of the locations in advance, and therefore searching for the postcodes or finding the coordinates on Google Maps took the same effort. The above is handy if the postcodes are known in advance, for example if you have a dataset containing post codes.

Initially I used Google Sheets to store the csv files and then accessed this through Python using the method described here. This was very easy, however it requires a local copy of my API key and therefore I have saved the coordinates offline in a csv file that is provided with the code on github.

Executing Python Calls in Julia

Julia has a very handy package called PyCall that provides the ability to directly call and interoperate with Python. This includes being able to import Python modules, call Python functions, define Python classes, and share large data structures between Python and Julia without copying them. I found this package very easy to setup, you have to set a few environment variables, and use. To import a Python module you use

using PyCall
fol = pyimport("folium")

You can then use the folium package, for example

m = fol.Map(tiles="OpenStreetMap",location=(median_lat, median_long), zoom_start=14)

creates a map centred at (median_lat, median_long). I only used PyCall when I was unable to find a solution in native Julia. In this case I used it for making calls to Openrouteservice and for creating maps using folium.

Calculating the Distance Matrix

The coordinates of the taprooms can easily be read into Julia using

csv_filename = "Data/LatLon.csv"
csv_Data = CSV.read(csv_filename,header=true)

and the next step is to calculate the distance matrix using Openrouteservice. The first step is to sign up and get an API key. Once we’ve imported the Openrouteservice modules into Julia using PyCall

ors = pyimport("openrouteservice")
req = pyimport("requests")

we can send routing requests. Note there are limits to how many requests you can make, however we will be well under this for our application. To send the routing requests and get the distance matrix we simply put our API keys in a header, put the coordinates in a body and use the following

call = req.post("https://api.openrouteservice.org/v2/matrix/foot-walking", json=body, headers=headers)
data = call.json()
dist_array = data["durations"]

In this case we are specifying that we are walking between locations and the distance array is returned with length of time to walk between each point. I have included an image of the distance array below. The values are in seconds to walk between each place and the diagonal values are all 0’s. Distance Array

Calculating the Optimal Route

I used the TravelingSalesmanHeuristics package for Julia. This takes as input a distance matrix and a quality factor, which determines what algorithms to use, and returns an approximation of the optimal path. A higher quality factor does not necessarily return a better solution than a lower quality factor but it will increase the computation time. Due to the relatively small size of my problem I decided to use the maximum quality factor. I did try changing this parameter, and there was a small difference in the value of the objective function, but the computation time was always much less than 1 second regardless, so I kept it at 100.

How does this algorithm work? Looking at the code on github, the quality factor affects with algorithms to attempt. In all cases it starts with the farthest insertion method. This is a route construction method that generates a sub-tour adds the point that is furthest away from all points in the sub-tour and finds the optimal position for that point in the sub-tour until all points have been added.

The algorithm then moves on to the nearest neighbour algorithm, it will either perform this repetitively, changing the initial location at each iteration, or only once. Setting the quality factor $\geq 60$ will also apply the 2-opt algorithm to the returned path at each iteration. The algorithm then runs the furthest insertion again, this time either repeatedly with 2-opt, or a single time with 2-opt applied. The final route construction algorithm applied is the cheapest insertion algorithm, either repeatedly or a single time depending on the quality factor. Again the 2-opt method is applied in both cases. The final algorithm applied is the simulated annealing method, starting with the shortest route found so far. Subsections of the route are randomly chosen and reversed in order, if the cost is reduced then the new route is used. If the cost is increased then the route may still be chosen if the exponential of its negative magnitude divided by the current temperature is greater than a uniformly distributed random number between 0 and 1. Initially the temperature is high and therefore the probability of accepting the new route is high, however the temperature decreases at each iteration following an exponential decay and therefore this probability reduces with increasing iteration number.

The call to generate the route and time the algorithm is given below.

@time path, cost = solve_tsp(dist_array; quality_factor = 100)

Failing to Calculate the Optimal Route in Python

I initiall wrote this code in Python and spent a long time trying and failing to estimate the optimal walking route using mlrose and Google OR-Tools. Neither provided a solution that was close to optimal despite a significant amount of testing. I’ve included the code below for both, I’m sure there’s an obvious reason why these did not work, however I could not fix it.

# The mlrose method
import mlrose
fitness_dists = mlrose.TravellingSales(distances = dist_array)
problem_fit = mlrose.TSPOpt(length = n_breweries, fitness_fn = fitness_dists,maximize=False)
best_state, best_fitness,curve = mlrose.genetic_alg(problem_fit, mutation_prob = 0.2, max_attempts = 10, random_state = 2,pop_size = 1000, curve = True)

# The ortools method, a little bit more involved
from ortools.constraint_solver import routing_enums_pb2
from ortools.constraint_solver import pywrapcp
g_data_array = {}
g_data_array['distance_matrix'] = distance_array*100
g_data_array['num_vehicles'] = 1
g_data_array['depot'] = 0
manager = pywrapcp.RoutingIndexManager(len(g_data_array['distance_matrix']),
                                           g_data_array['num_vehicles'], g_data_array['depot'])
routing = pywrapcp.RoutingModel(manager)
def distance_callback(from_index, to_index):
        """Returns the distance between the two nodes."""
        # Convert from routing variable Index to distance matrix NodeIndex.
        from_node = manager.IndexToNode(from_index)
        to_node = manager.IndexToNode(to_index)
        return int(g_data_array['distance_matrix'][from_node][to_node])
transit_callback_index = routing.RegisterTransitCallback(distance_callback)
routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)
search_parameters = pywrapcp.DefaultRoutingSearchParameters()
search_parameters.first_solution_strategy = (routing_enums_pb2.FirstSolutionStrategy.AUTOMATIC)
search_parameters.local_search_metaheuristic = (
    routing_enums_pb2.LocalSearchMetaheuristic.GUIDED_LOCAL_SEARCH)
search_parameters.time_limit.seconds = 30
search_parameters.log_search = False
assignment = routing.SolveWithParameters(search_parameters)

Mapping the Optimal Route

After calculating the optimal route order, I performed another call to Openrouteservice to get the walking directions of the route. The first step was to reorder the coordinates of the points so that they were in the optimal route, this performed using the map function. I then put these into a dictionary and made a directions call to the Openrouteservice (recall, last time I used a matrix call). Note that path_reorder is the optimal path reordered so that it starts and ends at Piccadilly Station.

optimal_coords = map((i,j)->(i,j),csv_Data.longitude[path_reorder],csv_Data.latitude[path_reorder])
opt_body = Dict("coordinates"=>optimal_coords)
call = req.post("https://api.openrouteservice.org/v2/directions/foot-walking/geojson", json=opt_body, headers=headers)
data = call.json()
println("Total Walking Time calculated using TSP = $(data["features"][1]["properties"]["summary"]["duration"] / 60)")

The directions, an array of coordinates marking every time a change in direction is required, is contained in points_temp = data["features"][1]["geometry"]["coordinates"]. These can then be mapped to generate not only the optimal ordering but the optimal routing as well. To map the route I used the Folium package in Python, calling it using PyCall as before. I did think of using the OpenStreetMapX package built for Julia however this required downloading the section of the map that I needed, reducing the generalisability of the code, and it uses Folium anyway.

I generated a map using Folium centred on the median coordinates of the points

m = fol.Map(tiles="OpenStreetMap",location=(median_lat, median_long), zoom_start=14)

based on the OpenStreetMap. I then iterated through the locations and created an icon for each point to be shown on the map. Clicking on each icon shows the coordinates and name of the location.

for row in eachrow(csv_Data)
    name = row.brewery
    lat = row.latitude
    lon = row.longitude
    popup = @sprintf "%s\nLat: %.7f\nLong: %.7f" name lat lon;
    icon_type = "beer"
    if (name == "Piccadilly Station")
        icon_type = "train"
    end
    icon = fol.map.Icon(color="lightgray",
    icon_color="#b5231a",
    icon=icon_type, # fetches font-awesome.io symbols
    prefix="fa")
    fol.map.Marker([lat, lon], icon=icon, popup=popup).add_to(m)
end

After generating a map, I added a line showing the optimal route. The first thing to note is that Openrouteservice requires the coordinates in (Long,Lat) format, while Folium requires them in (Lat,Long) format. Therefore I swapped the columns of the array prior to calling Folium again. The map is saved out to a html file.

points_temp = data["features"][1]["geometry"]["coordinates"]
points = zeros(size(points_temp))
points[:,1] = points_temp[:,2]
points[:,2] = points_temp[:,1]
fol.PolyLine(points, color="red", weight=2.5, opacity=1,name="Optimal Brewery Crawl",overlay=true).add_to(m)
m.add_child(fol.map.LayerControl())
m.save("OptimalBreweryCrawl.html")

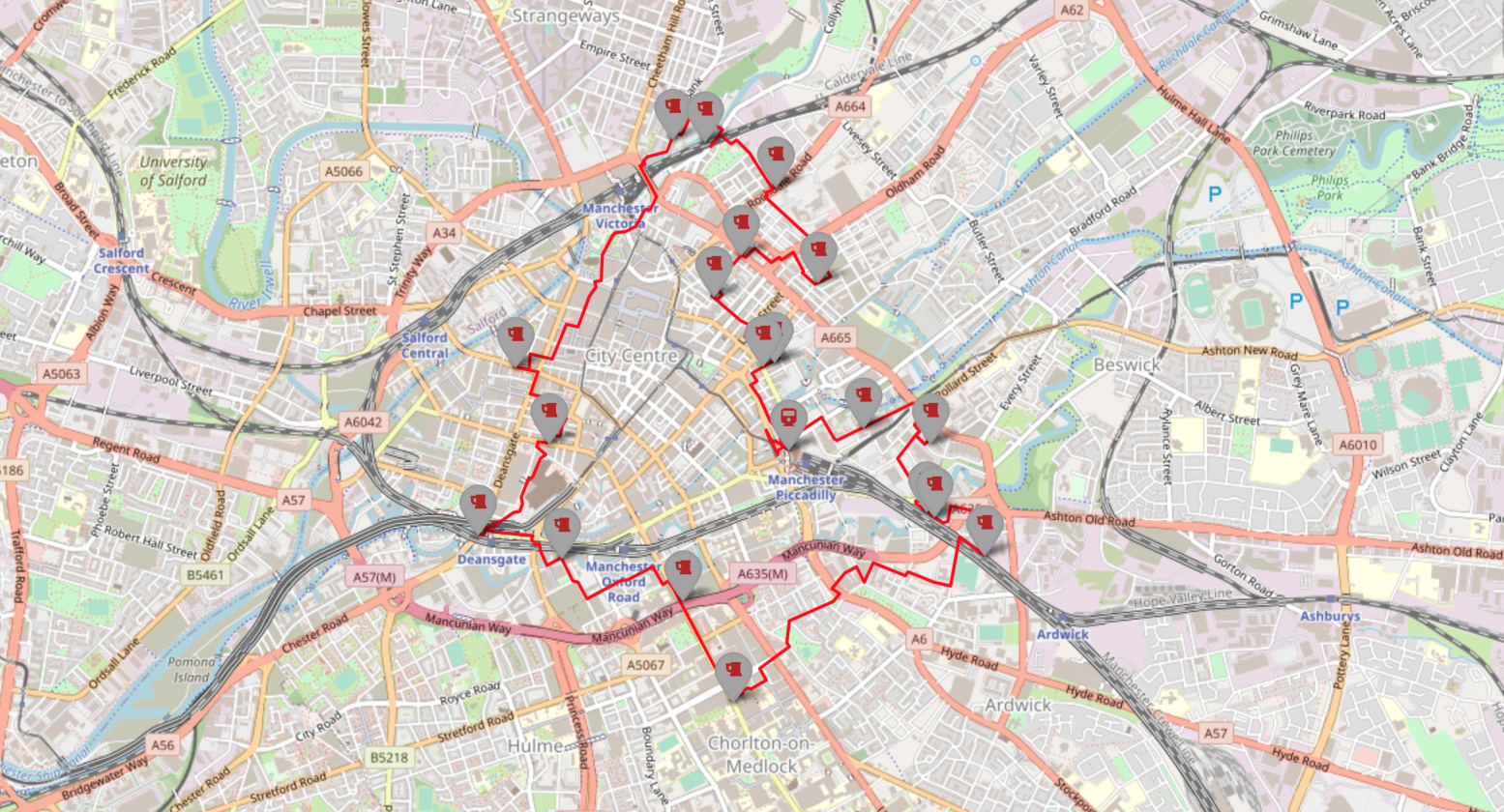
The Optimal Manchester Brewery Crawl

Now we can run the code and output the optimal route. The optimal route outputted by the code is

Piccadilly Station=>Beatnikz Republic Bar=>Northern Monk Refectory=>Thomas St Beerhouse=>Smithfield Market Tavern/Jack in the Box=>Seven Bro7hers=>Marble Arch=>Runaway=>Beatnikz Republic Brewery=>Gaslamp (Pomona Island)=>BrewDog=>Knott (Wander Beyond)=>Gasworks=>Ol=>BrewDog Outpost=>Beer Nouveau=>Manchester Union=>Alphabet Brewing Company=>Cloudwater=>Track/Squawk=>Piccadilly Station

and takes 146 minutes(2 hours and 26 minutes) to walk. The generated map is given below. Optimal Brewery Crawl

Conclusions

This was my first attempt at using Julia and I found it relatively easy to use as the syntax is similar to both Python and MATLAB. The Heuristics worked very well for solving this problem, however it is possible to solve the direct problem using Mixed Integer Programming. When I tested out this technique I found that the solutions were the same for both methods, however for larger problems (i.e. more locations) it may be that the exact method returns a better solution, but most likely at a greater compuation cost. The code from this post can be found here.